Utility Maximisation: A Guide to Rational Decision-Making

What is Utility Maximisation?

Utility maximisation refers to the concept that consumers seek to achieve the highest level of total satisfaction from their consumption decisions.

This concept explains how rational consumers behave while making economic decisions of consumption.

Understanding Utility

Before explaining the concept of utility maximisation in detail, let’s first explain a few basic terms used in utility analysis.

Utility

Utility refers to the satisfaction or fulfillment gained by a consumer from the consumption of a commodity.

Total Utility (TU)

Total utility refers to the total satisfaction gained by a consumer from the consumption of a given quantity of a commodity. It is calculated by adding the marginal utilities of all the units consumed.

TU = MU1+ MU2 + MU3 + …………. = ∑ MU

The rational consumers aim to maximise their total utility (TU).

Marginal Utility (MU)

Marginal utility (MU) refers to the additional satisfaction gained by a consumer from the consumption of an additional unit of a commodity. It is calculated by using the following formula.

MU = ∆TU/∆Q = (TU2-TU1)/Q2-Q1

Here,

∆TU = Change in total utility

∆Q = Change in the quantity consumed

TU1 = Initial value of total utility

TU2 = Final value of total utility

Q1 = Initial quantity consumed

Q2 = Final quantity consumed

Consumer Equilibrium

Consumer equilibrium refers to the state of a consumer when he/she gets maximum satisfaction from consumption of one or more commodities and there is no tendency to change that state.

Background

The concept of utility maximisation was developed by the philosophers Jeremy Bentham and John Stuart Mill and later incorporated into economics by the English economist Alfred Marshall.

Assumptions of Utility Maximisation

While explaining consumer behavior in utility analysis, the economists make the following assumptions.

The consumer is rational.
The consumption is continuous.
The units of all the commodities are homogeneous and of reasonable size.
The income of consumer is constant.
The prices of commodities are constant.

Approaches to Utility Maximisation

In economic theory, the topic of utility maximisation is discussed under the following two approaches.

Cardinal Approach

In this approach, utility is assumed to be a numeric figure and its unit of measurement is called ‘Util’. Moreover, if a consumer is consuming one product, then the law of diminishing marginal utility is used to explain utility maximisation. But, if consumer is consuming multiple commodities, then the law of equi-marginal utility is used to explain utility maximisation.

Ordinal Approach

In this approach, it is assumed that utility cannot be measured numerically. This utility is termed as ordinal utility. In this approach, utility maximisation is explained by using budget line and indifference curves.

Cardinal Approach: The Law of Diminishing Marginal Utility

The law of diminishing marginal utility is used to study consumer equilibrium when the consumer consumes one commodity only. According to this law, the total utility of a consumer will be maximum and the consumer will be in equilibrium, when the marginal utility becomes equal to the price of the commodity.

Suppose that the consumer is consuming good X, then his/her total utility will be maximum when MUx = Px. Here,

MUx = Marginal utility of good X

Px = Price of good X

This is illustrated by the following diagram.

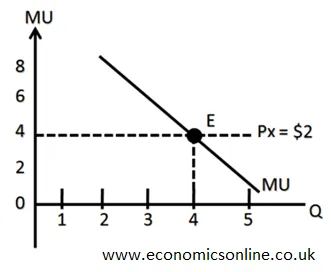
A graph illustrating utility maximisation under the law of diminishing marginal utility.

In the above diagram, Px=$2 and each $ spent on good X is giving 2 utils of satisfaction. The downward sloping marginal utility line shows that the initial units give higher marginal utility as compared the the later units. The consumer will be in equilibrium at point E and will be consuming 4 units of good X to get the highest level of satisfaction.

Cardinal Approach: The Law of Equi-marginal Utility

The law of equi-marginal utility is used to study consumer equilibrium when the consumer consumes multiple commodities. According to this law, the total utility of a consumer will be maximum and the consumer will be in equilibrium, when the marginal utility per $ will be the same for all the commodities consumed. For two commodities, the total utility of a consumer will be maximum when the following equation will be satisfied.

MUx/Px = MUy/Py

Here,

X and Y are the two goods which are consumed.

MUx = Marginal utility of good X

MUy = Marginal utility of good Y

Px = Price of good X

Py = Price of good Y

MUx/Px = Marginal utility per unit of money or marginal utility per $ from good X

MUy/Py = Marginal utility per unit of money or marginal utility per $ from good Y

Instead of good X and good Y, you can also assume two goods as apples and oranges.

Ordinal Approach: Budget Line and Indifference Curves

Budget Line

Budget line refers to a line which shows all possible combinations of two types of goods which a consumer can buy by using all of his fixed money income provided that prices are constant.

Assumptions

There are two goods X and Y.

The income of consumer is constant.

Px and Py are constant.

All the income is spent.

Budget Constraint

Budget constraint is an equation which gives all possible combinations of two types of goods, which a consumer can buy by using all of his fixed money income provided that prices are constant.

This equation is (Px) (Qx) + (Py) (Qy) = Money Income

Budget line is the graph of the budget constraint and this graph is shown below.

A graph of budget line.

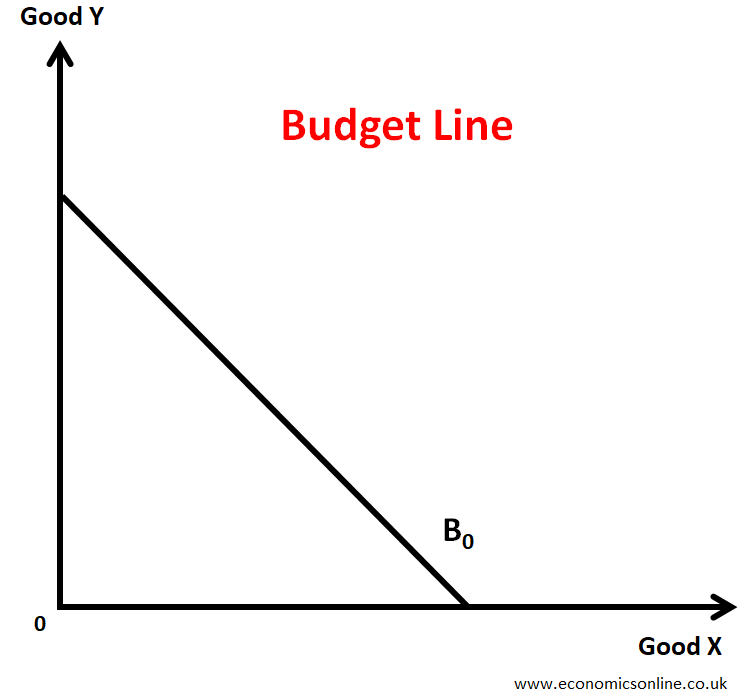
A consumer will move along the same budget line due to change in preferences.

Indifference Curves

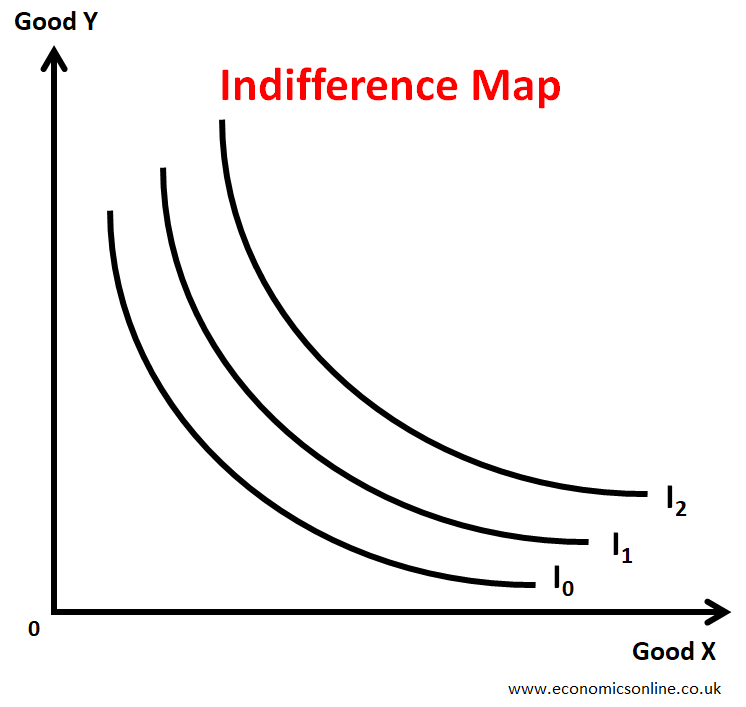
An indifference curve refers to a curve which shows possible combinations of two goods which consumer can consume to get same total satisfaction, hence, the consumer will be indifferent.

A consumer has an indifference map which is the set or collection of indifference curves. An indifference map is shown below.

A graph of indifference map.

Condition for Utility Maximisation

Under ordinal approach to utility analysis, a consumer will be in equilibrium and the total utility of the consumer will be maximum when the budget line touches the outer-most indifference curve.

This happens at the utility maximizing point E where the budget line is tangent to the indifference curve I1, as shown by the diagram below.

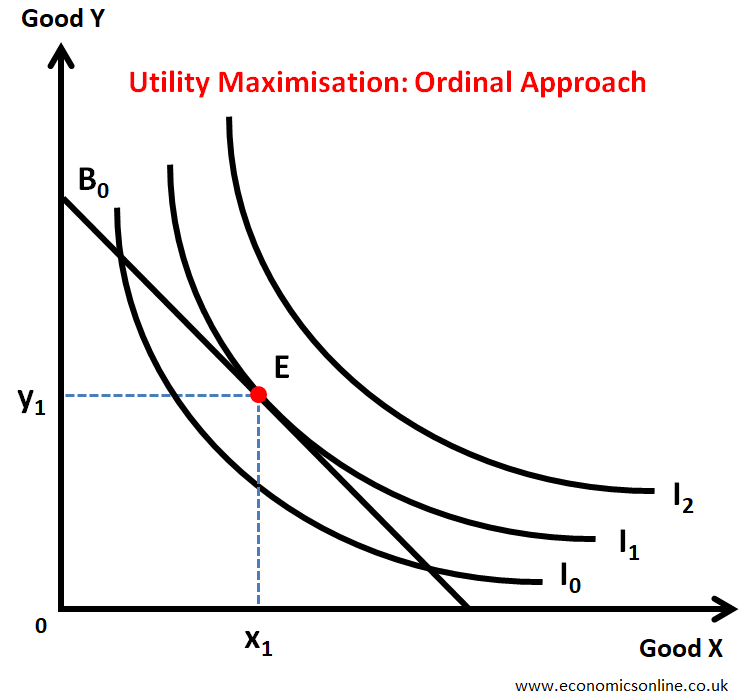
A graph illustrating utility maximisation under ordinal approach.

So, in ordinal approach, a consumer will get maximum total utility by consuming x1 quantity of good X and y1 quantity of good Y.

Conclusion

Utility maximization is a fundamental, yet, crucial concept in economics that underpins rational decision-making. By understanding how individuals seek to maximise their total satisfaction or total utility within the constraints of fixed prices and limited income, we gain valuable insights into human behavior and the process of rational decision-making.