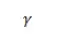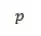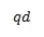Point Elasticity of Demand

Arc and point elasticity of demand

Arc elasticity

Arc elasticity of demand (arc PED) is the value of PED over a range of prices, and can be calculated using the standard formula:

More formally, we can say that PED is the ratio of the quantity demanded to the percentage change in price.

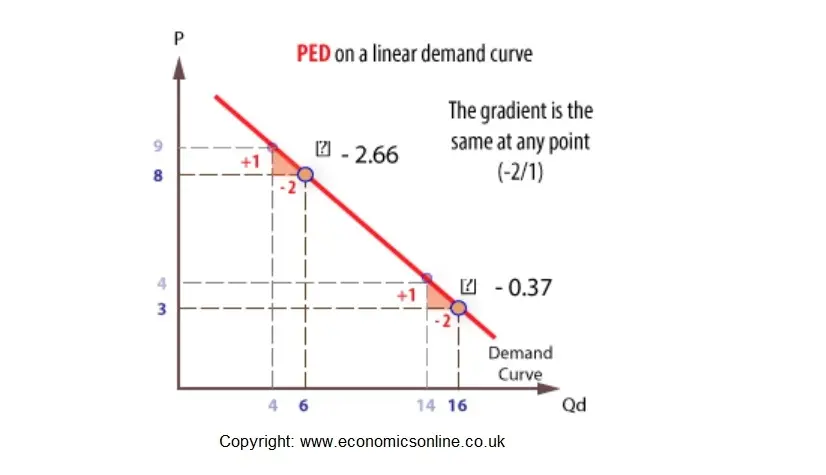
Point elasticity

Point elasticity is the price elasticity of demand at a specific point on the demand curve instead of over a range of it.

To get point PED we need to re-write the basic formula to include an expression to represent the percentage, which is the change in a value divided by the original value, as follows:

We can then invert the denominator, to get:

Elasticity has now been spilt into two parts, the

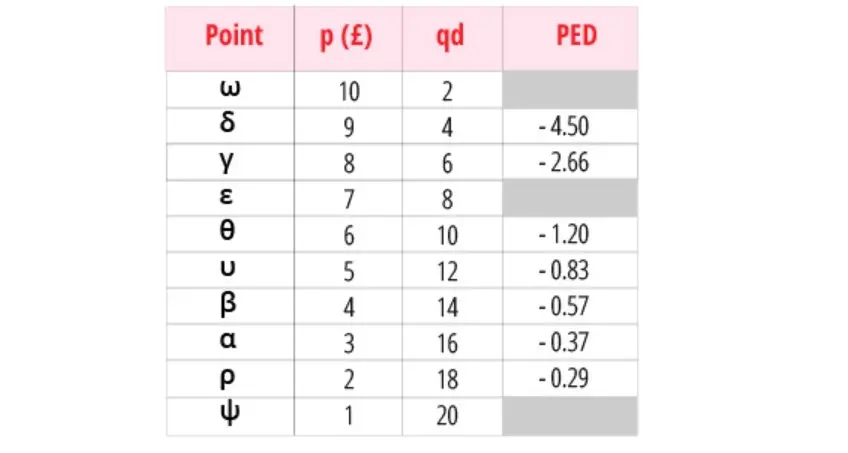
Example

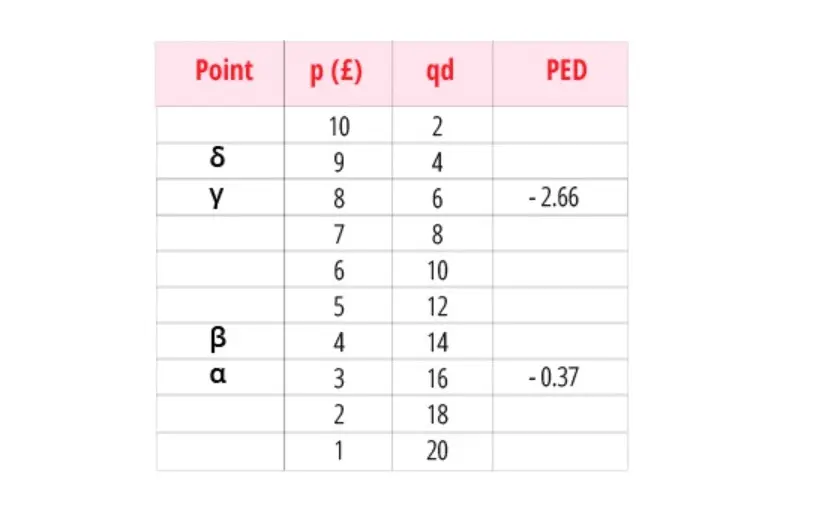
For example, consider the demand schedule for a hypothetical product. We can now calculate the point elasticity at point

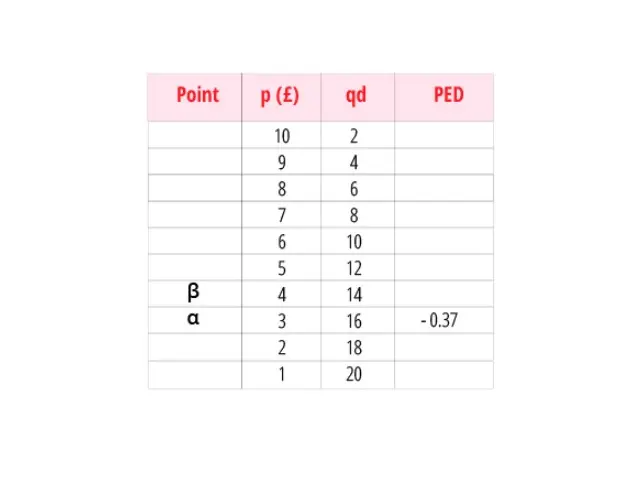
We can repeat this for point

初めて衣装を用意する際は、必要な付属品と別途準備するものを先に整理すると進めやすくなります。用途に合う候補を整理するときは、アロナ コスプレ衣装で商品内容を見比べられます。最後に衣装全体を試着し、正面だけでなく横や後ろからもシルエットを確認すると安心です。